Roulette, An Intelligent Negotiating Agent Jan. 9, 2018 in Algorithms, Java, Text, University
When making decisions, people negotiate to maximise utility and social welfare - agents are no different. Utilizing the GENIUS framework, this report tests time dependent concessions, and fitness proportionate selection putting them to test in a negotiation competition. The results are analysed and discussed.
- CSS Concept: Computing methodologies → Intelligent Agents
- Keywords: Agents, Negotiation, Competition, Selection, Roulette
Introduction
Our team was tasked with producing a negotiating agent to compete in a tournament run within the GENIUS framework 1. The agent needed to explore and negotiate inside an unknown domain, against an uncertain quantity of agents, to reach an agreement maximising both utility and social welfare. It is no good producing an entirely selfish agent 2!
Negotiations use the Stacked Alternating Offers Protocol 3, with a timeout of 180 seconds. In this scenario utility remains constant, however time is limited so it was decided that it would be a good idea to become more agreeable as time passed. From there, randomness is used to both confuse opponents, and to build up counteroffers.
Altogether, this produced a good, if flawed agent, which will now be discussed further.
Modelling Time
To ensure that agents remain generic, the GENUIS framework only reports time normalised between 0 and 1 4. Rounds and turns can be counted with an incrementing integer:
time = this.getTimeLine().getTime();
round = round + 1;If needed, an agent could determine either the time or round limit on their second round by waiting a predetermined amount of time, asking for the new time, and comparing:
Agent Utility
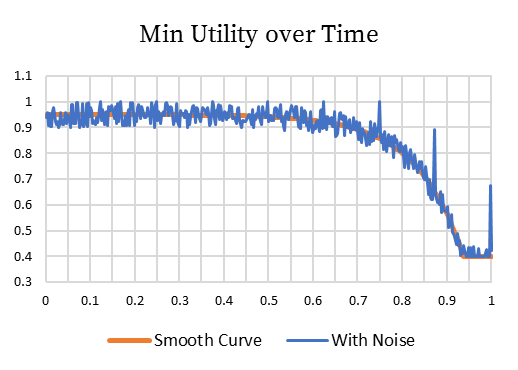
However, this strategy renders such techniques pointless. Unlike more complicated agents which may concede more if opponents concede and vice versa so may need to know this, this agent uses the simpler strategy of decreasing Utilitymin over Time. From testing, this strategy is easy to implement and rather successful in practise.
Additionally, random spikes are added, on average, every 25 rounds to try and confuse certain types of opponents.
Negotiation was cut-off at 0.4 to provide a floor and not reward agents only accepting maximum bid. In typical negotiations, it was decided that a competent agent should be able to come to an agreement where each agent gets at least 0.4 utility.
However, looking at the results, 0.4 may have been a mistake as the agent only managed 86%, 71%, and 75% acceptance. A lower value of 0.2 may have raised the agent’s agreeability. Alternatively, a focus on exploration could have proven useful.
Accepting Offers
The agent decides whether to accept an offer if it is greater than or equal to Utilitymin, otherwise it proposes an offer. As time passes, Utilitymin decreases meaning that the agent is more likely to accept.
Proposing Offers
The agent is designed to make use of frequency analysis 5 and fitness proportionate selection 6 to learn opponent behaviour as it negotiates. This allows it to make good offers that are both beneficial, and maximise social welfare. To start it prefills a frequency table by evaluating each option, and multiplying it by a prefill multiplier. This step allows the agent to fully explore the utility space, and make good bids.
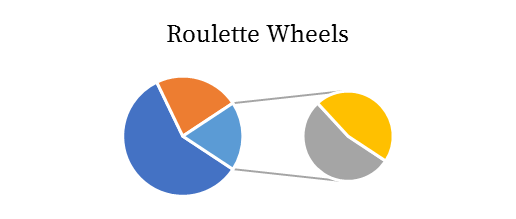
When it is the agents turn to propose, it evaluates each option for each issue, storing the result in an inner ‘roulette wheel’.
This inner wheel is then added to an inverted outer wheel. This inversion causes the issues the agent cares less about (lower total evaluation), to mutate more, and when they do mutate, they are more likely to land on values that the agent wants (higher evaluation).
Now the agent spins, and spins, and spins until it either times out, or the utility of the offer falls within a 0.1 wide utility window.
Fitness Proportionate Selection
But what is fitness proportionate selection? It is an operator used to make selections in genetic algorithms 7. Given a list of options, each is evaluated for fitness, and thus probability.
Below is a Java implementation. Pass in a fitness array, and it returns the index of the selected option.
public int roulette(double[] v) {
double c = Math.random() * Arrays.stream(v).sum();
for(int i = 0; i < v.length; ++i)
if ((c -= v[i]) <= 0) return i;
return v.length – 1;
}To form a bid, the agent takes the maximum bid and mutates it with fitness proportionate selection until it fits within a 0.1 wide utility window, or it times out. This is the proposal.
Integers and Reals
For completeness sake, the agent has a simple algorithm for integers and real numbers where it simply uses the Utilitymin as lerp time. So, at time zero it proposes the max bid, and at time one it proposes lerp(maximum bid, average, 0.4). This functionality is not strictly necessary, but as it does not hurt the agent, it is nice to have for completeness sake.
Agent Tuning
The agent has several parameters to tune that influence its negotiating behaviour. Different combinations of values were tested, done inside a tournament versus half a dozen or so other agents. This helped eliminate noise and hopefully not over tune the agent:
- Stubbornness – Controls concession speed.
- MinimumUtility – How low the agent will go.
- PrefillMultipler – How quickly the agent learns.
- RandomFrequency – Random spikes frequency.
- IssueBias – Used to invert a wheel.
Testing the Agent
The agent was tested against a mixture of agents including some of the very best agents from previous competitions 8. However, the selection was heavily biased towards very good agents, which try to maximise social welfare. This let flaws in the agent to go unnoticed, until it was too late. Testing should have included a better variety of agents, on more domains.
Before submitting it was tested against another groups agent, sharing logs between teams. The shared agents were deleted immediately afterwards, with no copies made.
| Mean Utility | Mean Pareto | Mean Nash | Mean Welfare | Sum Utility | Sum Welfare | Mean Rounds | |
|---|---|---|---|---|---|---|---|
| TheOther | 0.7547 | 0.09777 | 0.3714 | 2.192 | 95.09 | 276.2 | 373.4 |
| Roulette | 0.7116 | 0.02245 | 0.2901 | 2.340 | 89.67 | 295.0 | 411.5 |
| AgentHP2 | 0.7462 | 0.02528 | 0.2773 | 2.344 | 94.02 | 295.3 | 395.8 |
| Grandma | 0.7797 | 0.01973 | 0.2779 | 2.360 | 98.24 | 297.4 | 383.6 |
| Caduceus | 0.7479 | 0.09839 | 0.3224 | 2.220 | 94.23 | 279.7 | 445.2 |
| Group2 | 0.9042 | 0.02367 | 0.3179 | 2.309 | 113.9 | 291.0 | 452.3 |
| Flinch | 0.6603 | 0.01926 | 0.3194 | 2.318 | 83.20 | 292.1 | 325.2 |
| Negotiator | 0.8389 | 0.03063 | 0.2830 | 2.347 | 105.7 | 295.7 | 425.6 |
| * | 0.7679 | 0.04215 | 0.3074 | 2.304 | 789.8 | 2322 | 401.6 |
While this agent could do better on utility, social welfare was good. It was decided that as the other group was good, and the agents that it competed against were good, it was ready to submit, it was ready to compete. This was a mistake.
Agent Performance
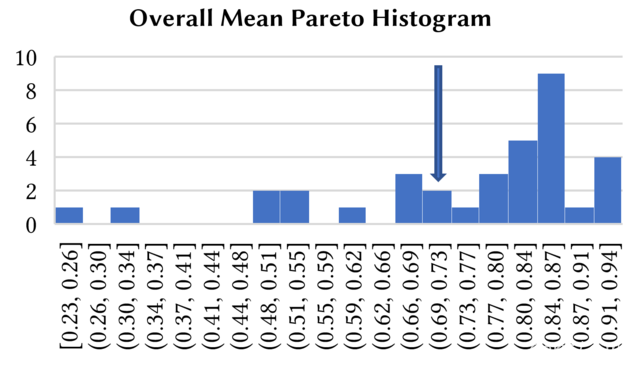
| Agreements | Mean Utility | Mean Pareto | |
|---|---|---|---|
| Small | 85.71% | 0.7841 | 0.7135 |
| Medium | 70.72% | 0.6224 | 0.6555 |
| Large | 75.45% | 0.6056 | 0.7462 |
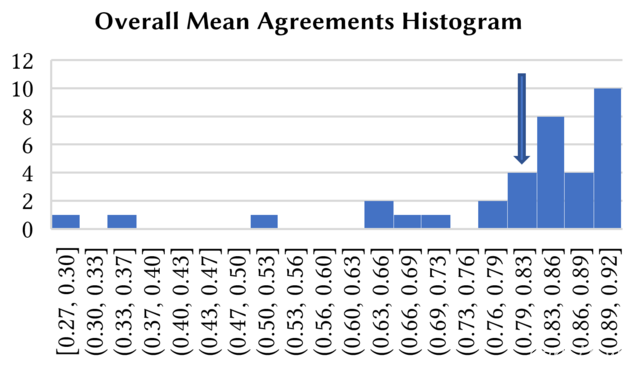
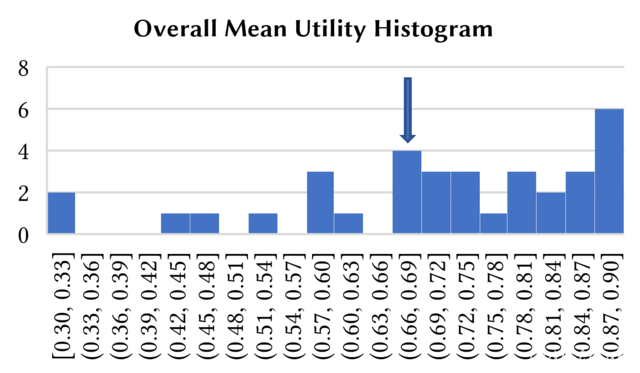
| Overall | 77.29% | 0.6707 | 0.7051 |
The agent did averagely, earning a total of 14/20 marks 9.
While agreeability was high, it was felt that it should have been higher. To improve, Utilitymin could have been lowered from 0.4, or the agent’s ability to explore could have been bettered.
Utility was too low, it appears the agent failed to truly learn.
Compared to others, this agent had a low mean Pareto distance.
Programming Failure
This agent is broken. While it promised to make use to frequency analysis and fitness proportionate selection, a small programming bug reduced it to a simpler agent. In its ‘crippled’ state, it performed averagely earning 14 marks out of 20 which according to the spec, corresponds to ~70% .
Due to a poor test design, this went unnoticed. However, it gracefully degenerated, leaving a functional, if boring agent.
Here is the bug:
Map<Integer,Map<String,Integer>> frequencies;
double freq = frequencies.get(id).get(name) / frequencies.get(id).get("_total_");In Java if operands are integers, division results in an integer:
Frequency therefore is virtually always 0, and so is score:
This zero propagates through the program, filling the roulette wheels with zeros. However, as the first wheel in inverted, the agent can make not terrible offers.
Roulette[
OuterWheel:
0.0,0.0,0.0
InnerWheels:
0.0,0.0,0.0,0.0
0.0,0.0,0.0,0.0
0.0,0.0,0.0,0.0
]
Fixing the Agent
Fixing the agent was incredibly simple, casting either the count or the total to a double instantly fixes the problem.
Roulette[
OuterWheel:
0.5125,0.5975,0.7087
InnerWheels:
0.5125,0.07480,0.1025,0.1117
0.08458,0.5975,0.4352,0.05320
0.1290,0.01526,0.7087,0.05929
]
However, running the fixed code did not result in any big improvements, and in some circumstances the fixed agent performs worse! This is likely because the new agent is not tuned, and with tweaking the fixed agent could beat the broken agent with ease.
Conclusion
In conclusion, while this agent was imperfect and flawed, it still managed to compete and win an average score. While it cannot be known if this strategy was the best for certain, the agent could easily be stripped of broken components, to produce a simple and effective agent in tens of lines of code.
Running the fixed agent against the submitted agent and others proved that while the implementation was flawed, the technique itself is sound. Frequency analysis and fitness proportionate selection is fast to run, quick to implement, and effective in negotiations.
The programming failure highlights the need to good testing with proper analysis where you check that each stage of the process works, not just the final output. Both static code analysis tools such as IntelliJ’s linter, and running it within the GENIUS framework failed to find the bug. Only by printing out the roulette wheels after submission was the bug found.
Overall, this project was a success. While the agent performed averagely, not all was lost. Our team discovered a very simple and quite effective technique, how to improve it, and highlighted the need for in-depth testing.
References
R. Lin, S. Kraus, T. Baarslag, D. Tykhonov, K. Hindriks and C. M. Jonker, “Genius: An Integrated Environment for Supporting the Design of Genric Automated Negotiators,” Computational Inteligence, 2012. ↩
E. H. Gerding, “Intelligent Agents Coursework Specification,” 1 12 2017. Available: https://secure.ecs.soton.ac.uk/notes/comp6203/2017/comp6203-2017-coursework.pdf. [Accessed 22 12 2017]. ↩
R. Aydogan, D. Festen, K. V. Hindriks and C. M. Jonker, “Alternating Offers Protocols for Multilateral,” Delft University of Technology, Delft, The Netherlands, 2016. ↩
T. Baarslag, W. Pasman, K. Hindrik, D. Tykhonov, W. Visser, M. Hendrikx and D. Feirstein, “Negotiation User Guide,” Delft University of Technology, Delft, The Netherlands, 2017. ↩
L. R. Weingart and M. O. a. P. L. Smith, “Quantitative Coding of Negotiation Behavior,” International Negotiation, vol. 9, no. 3, pp. 441-456, 2004. ↩
A. Lipowski and D. Lipowska, “Roulette-wheel selection via stochastic acceptance,” Adam Mickiewicz University, Poznań, Poland, 2011. ↩
E. Zitzler and L. Thiele, “Multiobjective Optimization Using Evolutionary,” in Lecture Notes in Computer Science, Berlin, Heidelberg, Springer, 1998, pp. 292-301. ↩
Delft University of Technology, “Automated Negotiating Agents Competition (ANAC),” 2017. Available: http://ii.tudelft.nl/negotiation/index.php/Automated_Negotiating_Agents_Competition_(ANAC). [Accessed 23 12 2017]. ↩
D. E. H. Gerding, “Results,” 21 12 2017. Available: https://secure.ecs.soton.ac.uk/notes/comp6203/2017/competition/results.pdf. [Accessed 22 12 2017] ↩
Re-learning the FluteHow to play Cheat, Sh*thead, and Cheathead